电机控制的高级技术

在工业和汽车应用中普遍存在的 BDC 电机依赖刷子进行换流。BDC 电机由定子、转子、刷子和整流子组成，可提供简单且成比例的速度和扭矩控制。不过，其寿命取决于负载、电流和振动等因素。 

隐患在于，刷子会随着时间的推移而磨损，并需要维护。此外，整流子和刷子会产生电尖峰，因此禁止在工作环境存在易燃气体或存在火灾危险的应用中使用。图 1 显示了 BDC 电机磁通方案，其中整流子和刷子会机械管理电机磁通方向，以保持转子移动。 

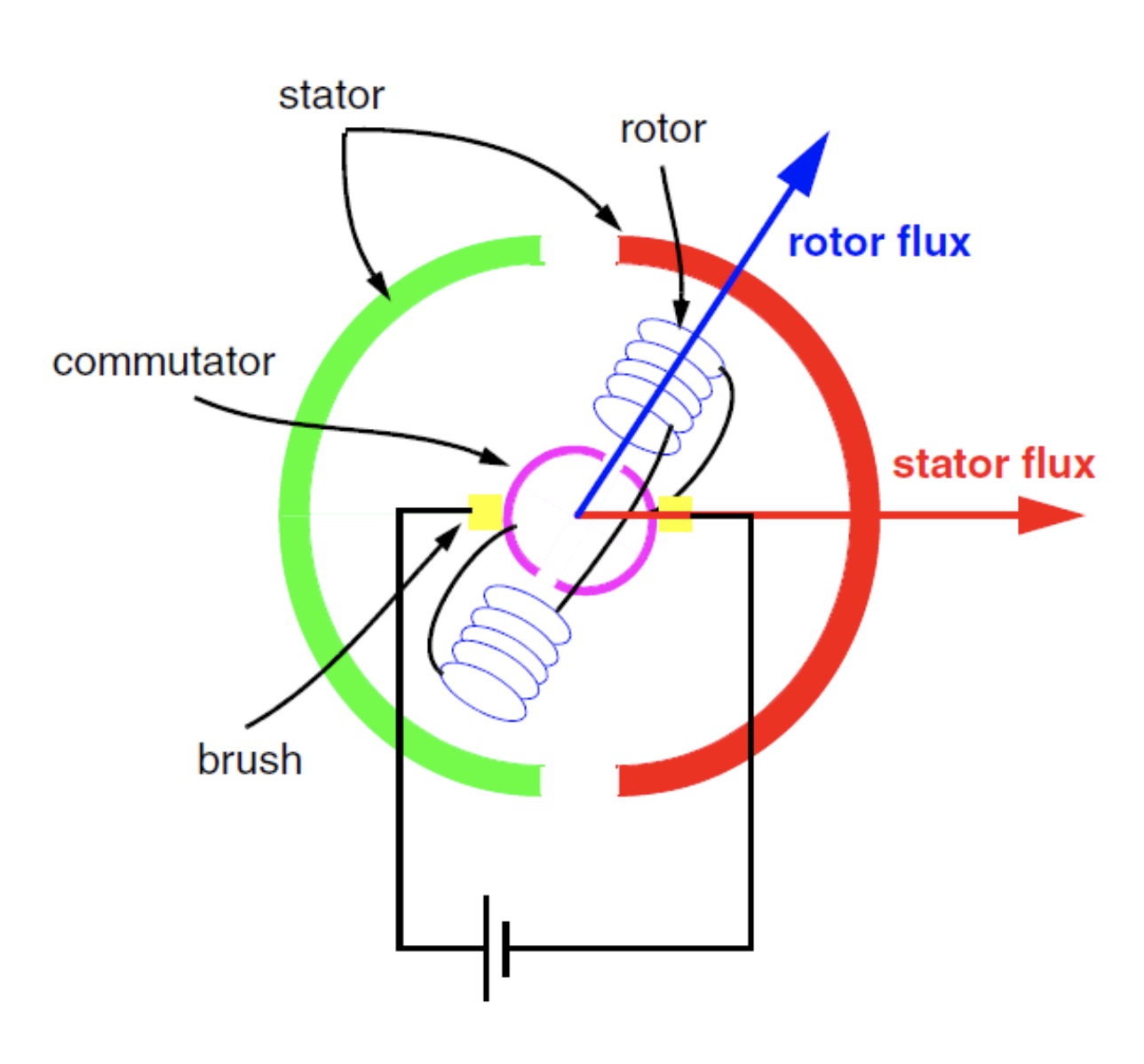
图 1：BDC 电机磁通方案。

尽管容易产生维护（或更换）成本，但由于其吸引人的价格和简便的操作，BDC 电机长期以来一直是汽车市场中小型执行器的首选解决方案，不过值得注意的是，随着越来越多的公司转向 BLDC 电机，这种价格优势不再始终成立。

对于这类机器而言，为了控制扭矩，只需调整施加的电压即可。因此推导出的最基本的控制方法形式，称为 V/f。这种方法假设气隙磁通恒定，并将电机速度和电机电压线性关联。此类控制可以利用以下调制。 

脉宽调制（PWM）：

电动机扭矩与电流成正比，通过脉宽调制（PWM）调节电压来进行控制。高边 MOS（p 通道）为低电位有效，需要低电压才能激活。低边 MOS（n 通道）为高电位有效，需要高电压才能激活。具有相同 PWM 曲线的相反的 MOSFET，其同步需要反相逻辑。

图 2 所示的示例中，电动机 B 相位被负激活，而 A 相位被正激活，具备 20% 的脉宽调制占空比。

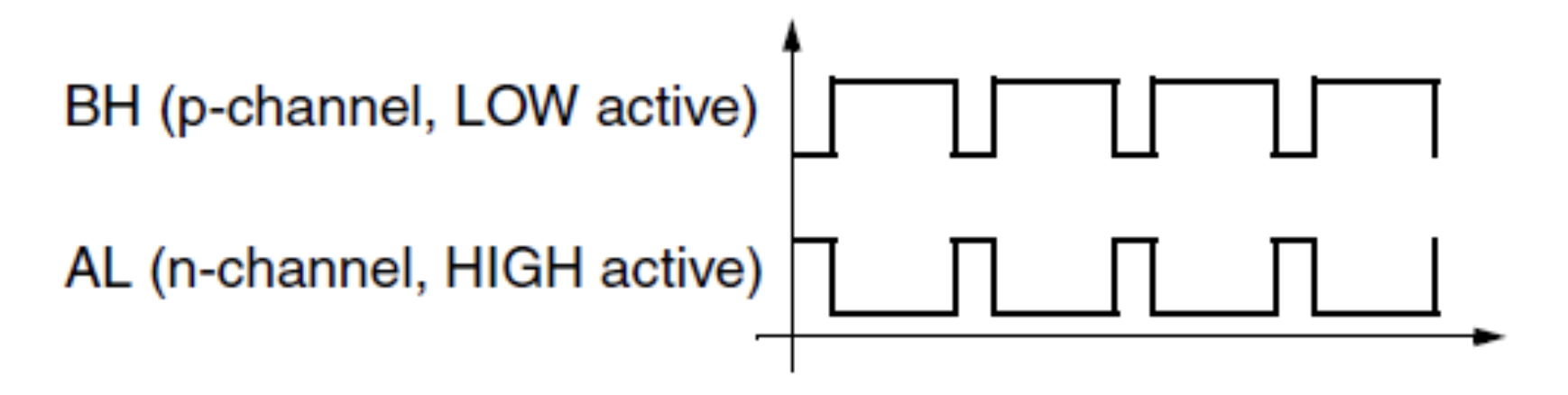
图 2：使用 P/N 通道半桥在电机相位激活期间实现输出反相逻辑。

为电动机相位通电的替代方法包括在整个持续时间内保持一个 MOSFET 100% 激活，并仅对另一个 MOSFET 应用 PWM 曲线。图 3 所示的这种技术也可以反向应用，其中 AH 已 100% 激活，BL 由 PWM 信号控制。

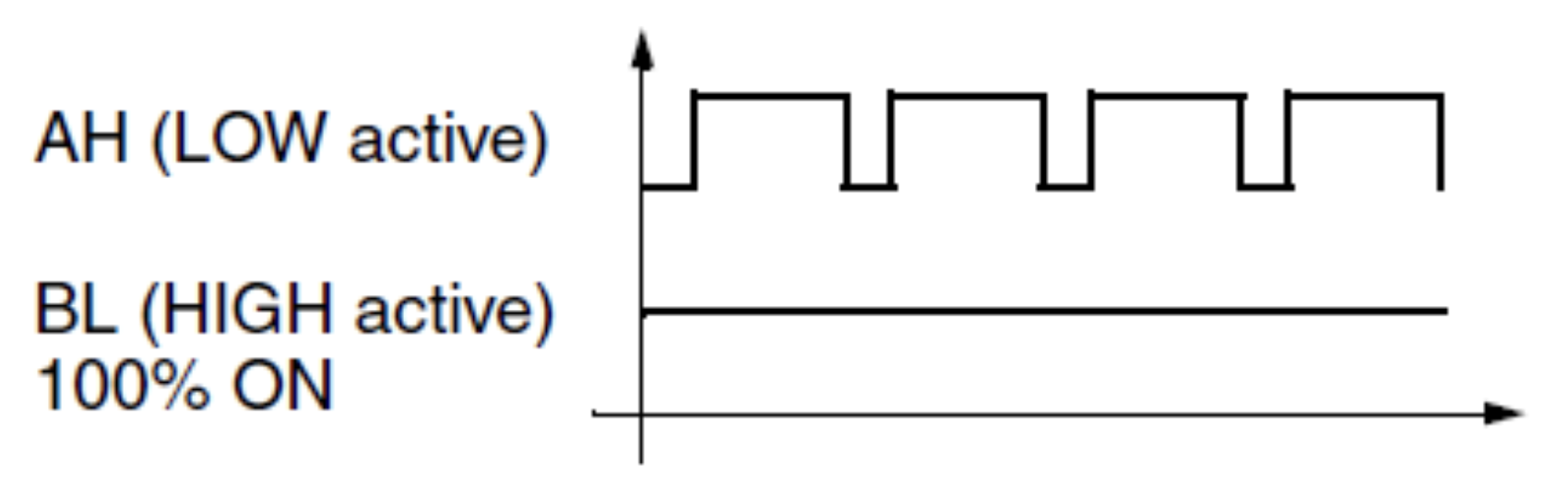
图 3：低边 MOSFET 100% 激活，而 HS 开关负责 PWM 调节。

BLDC 电机采用电子换流且无刷，具有高可靠性和高效率。转子上的磁铁、通电的定子线圈和电子换流有助于精确的扭矩控制。无滑动接触可以延长电机的寿命，而滚珠轴承是限制因素。

如前所述，在这种情况下，电子整流子是必须的，因为 BLDC 电机没有整流子和刷子。如图 4 所示，定子磁通应由适当的电压矢量产生，其方式是磁铁产生的转子磁通跟随电压矢量。 

本示例中，相位 A 正激活，相位 B 负激活，相位 C 保持开启，导致电机逆时针旋转（假设为前进方向）。这就导向了六步换相的解释。
 

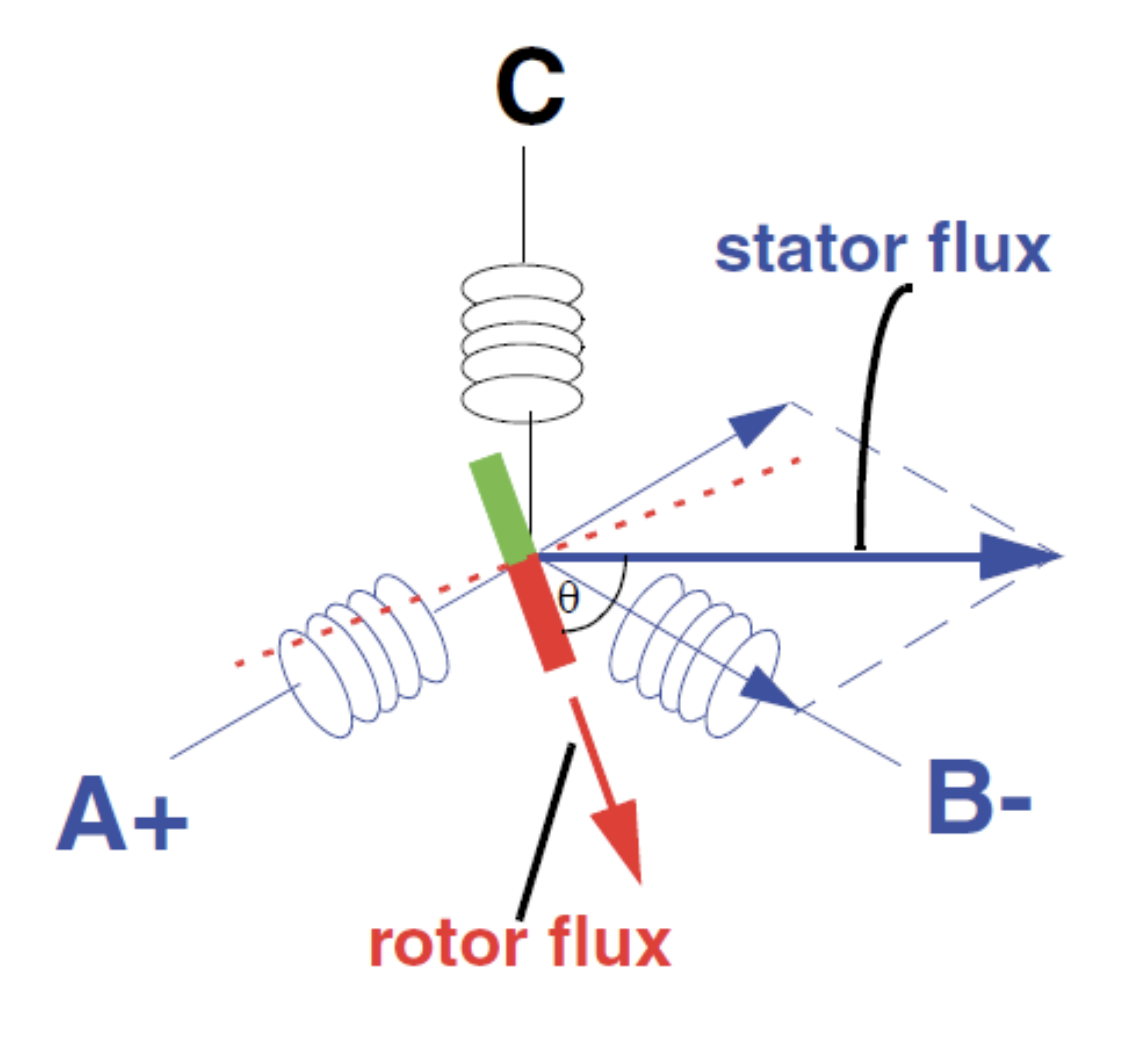
图 4：电机磁通方案，3 相 BLDC 电机

六步换相：

六步换相技术涉及一次为两个相位通电，同时在三相电机中保持第三相悬空（Hi-Z）。这种调制通常与 BLDC 电机结合部署，BLDC 电机非常适合此目的。由于六步换相的调制特性，人们发现，将 BLDC 的反电动势（BEMF）修改为梯形（而不是曲线形）将产生更稳定的扭矩，波纹更小（波动）。
 

图 5 展示了六步调制的换相矢量图。根据电机磁通位置落入六边形的哪个区域，选择合适的电压矢量。本示例描绘了顺时针旋转。如果选择了分区 0，则将应用矢量 V4。这会导致转子和定子磁通之间产生 120°的移相。矢量长度（振幅）由 PWM 的占空比控制。

了解电机磁通方向（转子位置）对于最佳性能至关重要，BLDC 电机通常会为此使用集成传感器或外部位置传感器。特殊技术（例如读取 BEMF）还可以通过过零点（ZC）检测转子位置，而无需传感器。
 

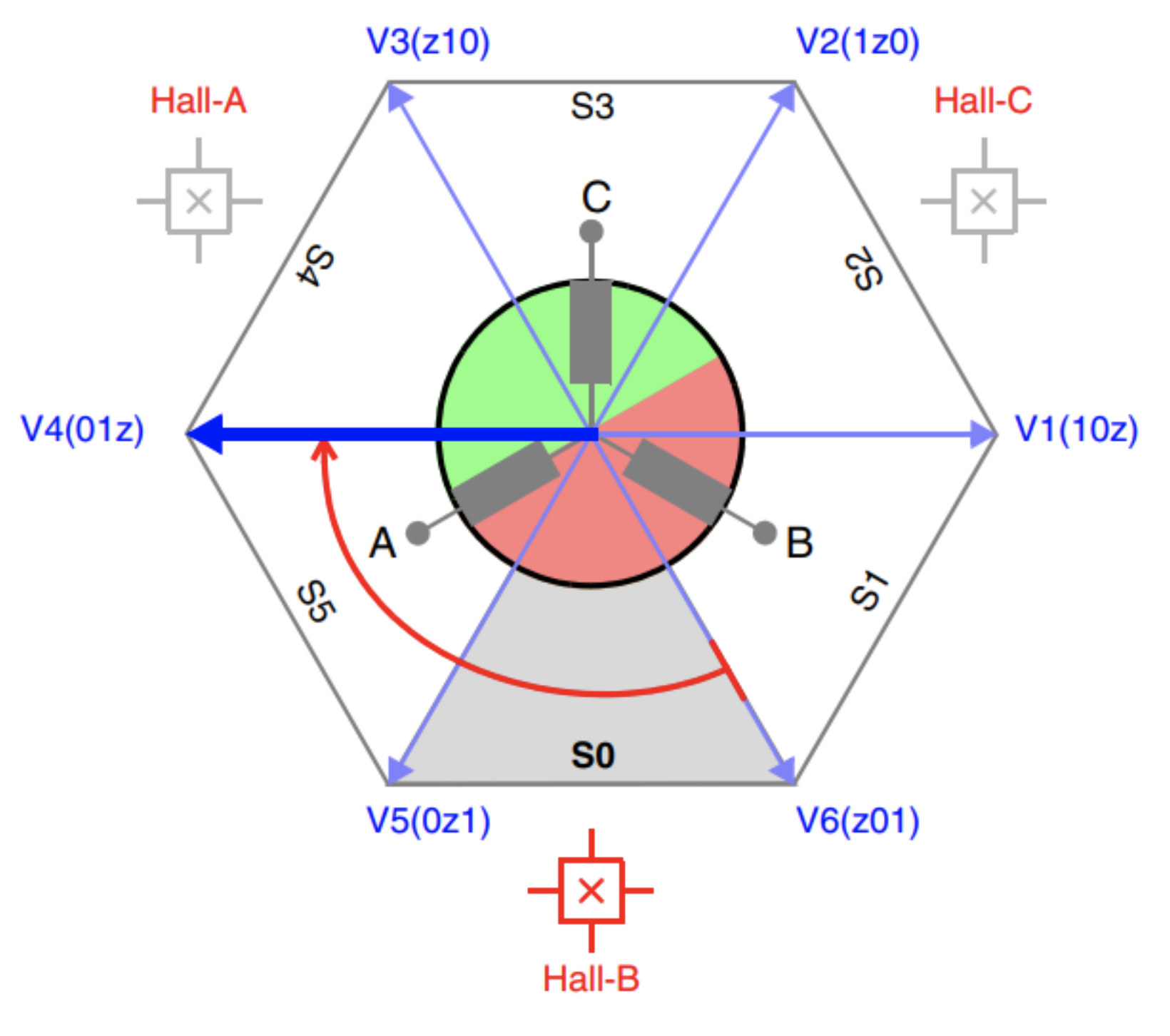
图 5：六步调制的换相矢量图表。

无感六步（ZC 检测）：

六步调制的固有特征可支持直接感测悬空相位，从而使控制器能够检测到 ZC 瞬间。这个概念需要一台具备 Y 形连接的定子线圈才能工作。公共模式电压相当于中性点，并用作以悬空相位为输入的比较器电路的参考。每当悬空相位电压与虚拟中性点电压交叉时，即称为发生 ZC。每个分区都有一个预定义的模式，以实现正确的六步换相序列。只要将正确的悬空相位多路复用到单个比较器上，就足够了。 

图 6 描绘了 CCW 序列，并突出显示了分区 1 内转变的（ZC）瞬间。例如，如果在分区 1 中检测到相位 B 的 Zc，则算法知道 30 个电度后它应该让分区换流（电子换流），并将施加的电压分量从“1z0”更改为“z10”。
 

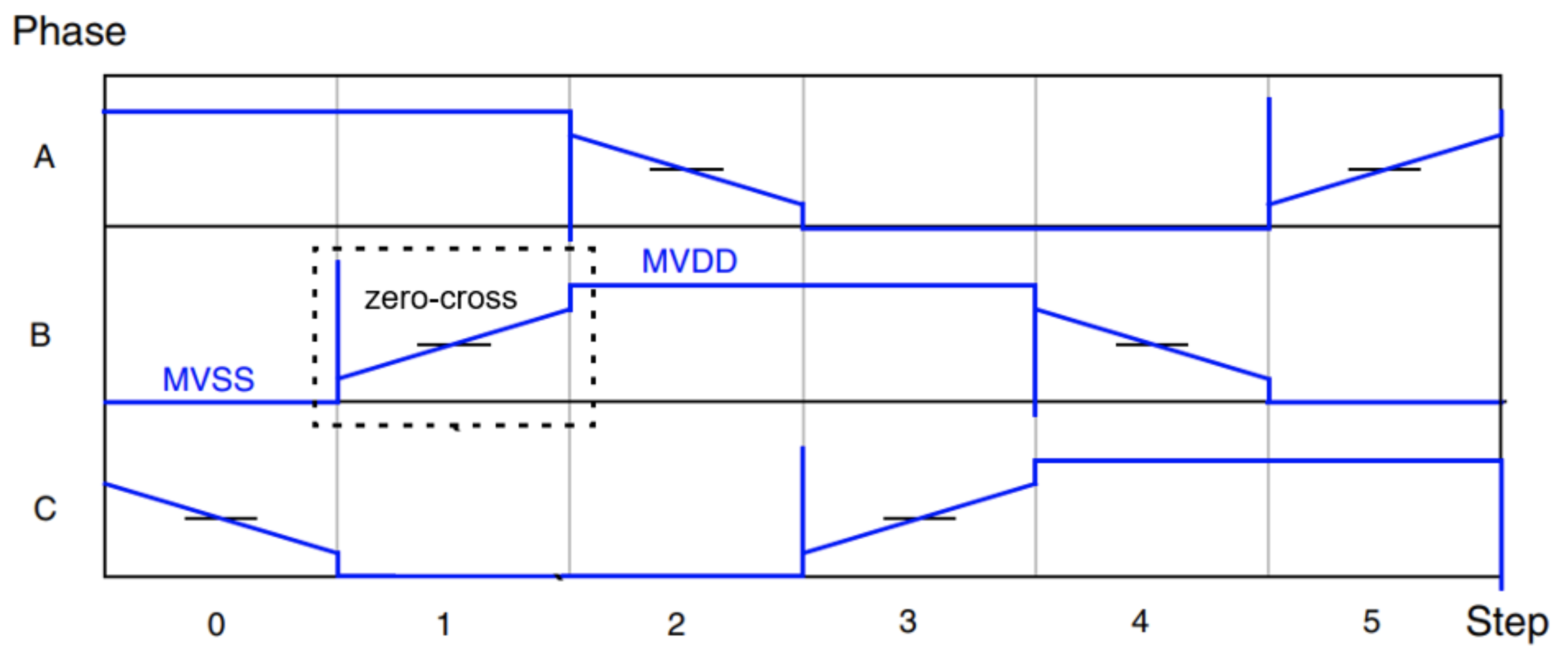
图 6：六步 CW 换相序列。

空间矢量调制（SVM）：

空间矢量调制（SVM）是一种用于通过三相电压源逆变器（VSI）产生曲线形状电压的技术。SVM 通常用于驱动 AC 感应电机、无刷直流电机（BLDC）和永磁同步电机（PMSM）。图 7 显示了顺时针旋转的示例。如果使用 SVM 输入了分区 0，那么也将应用 V4。但这会导致 90°的移相。 
 

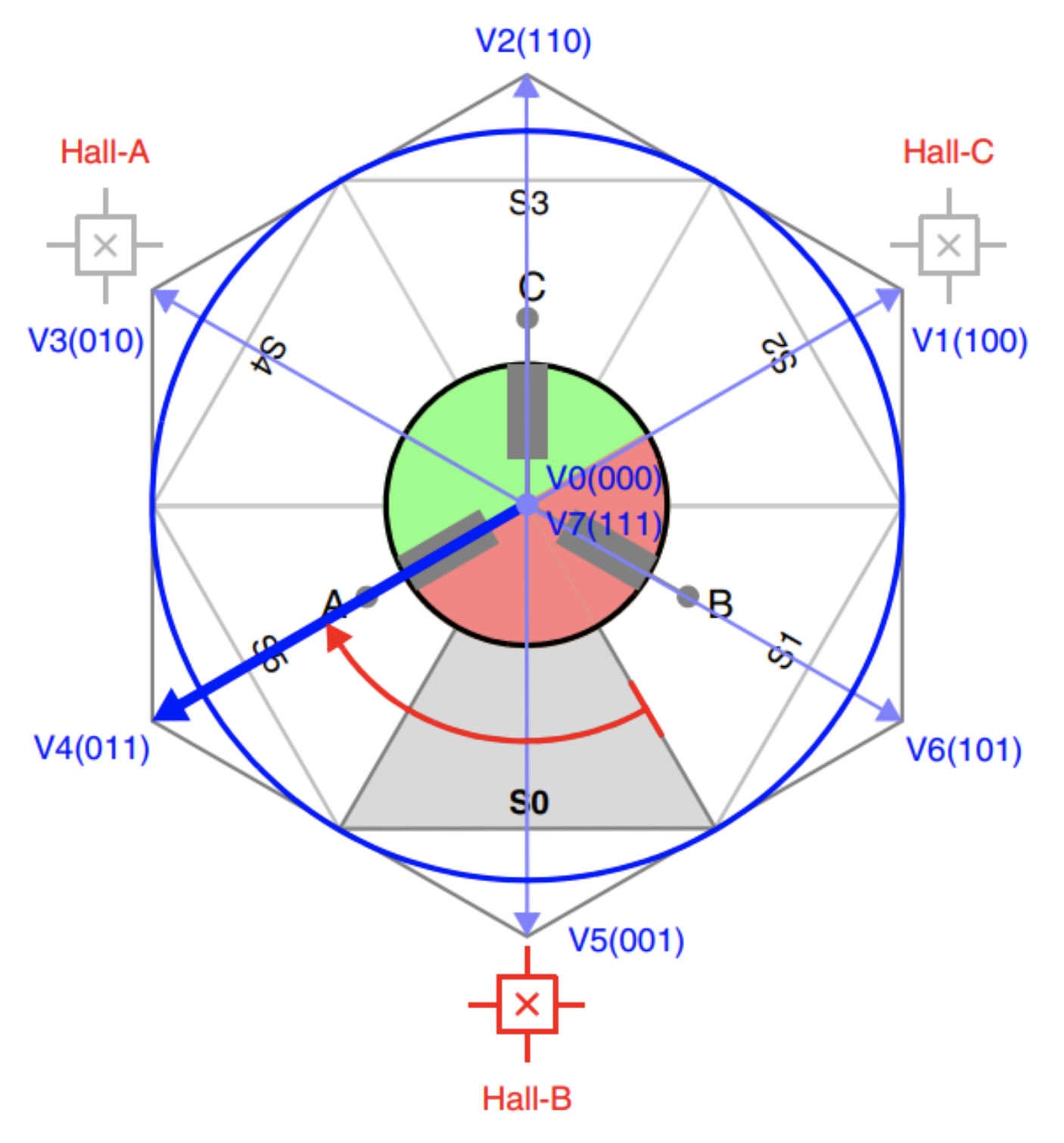
图 7：空间矢量调制的换相矢量图。

通过六步换相，定子磁场和转子磁场之间的移相仅维持 60°步。而利用 SVM，两个相邻矢量被时分复用，以便创建中间（平均）矢量。通过中间矢量，可以更精细地合成定子磁通方向，因而使 SVM 成为与高级控制方案配合使用的更合适的调制算法。

图 8 显示了中间矢量的结构。可以通过复用两个相邻矢量的分量 V_k  and V_k+1 来调整图 7 中矢量V_x 的方向。该矢量的绝对值（振幅）由零矢量 V_z （“000”或“111”）进行调整，这与方向不相关。停留时间 t_z' 越短，矢量振幅越高。在六边形中的任何位置，中间矢量都可以通过 (n - 1) · π/3 引用回到第一个分区。
 

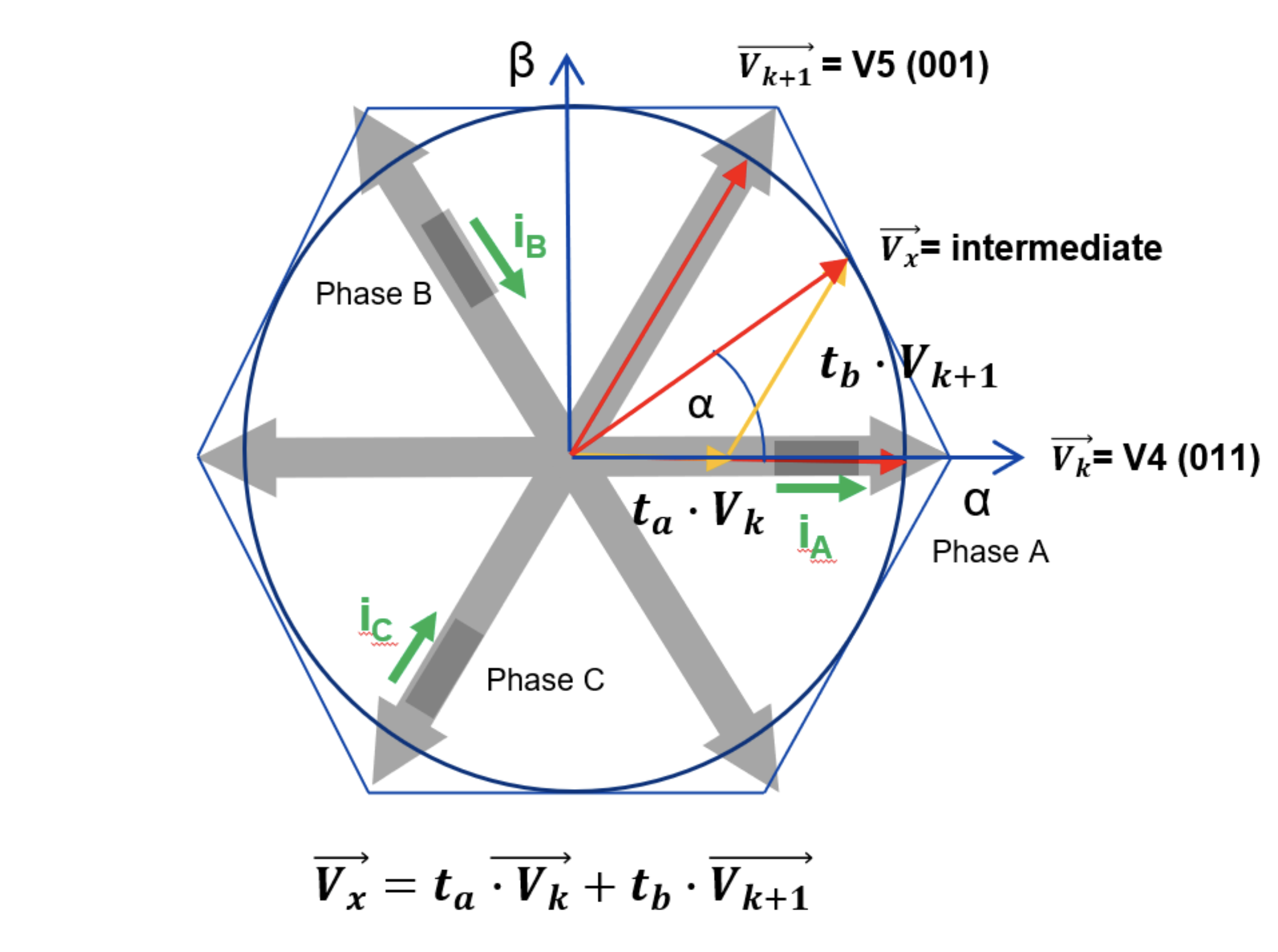
图 8：从 S5（V4）到 S0（V5）的中间矢量的 SVM 结构。

以下方程可用于根据实轴和虚轴上的电压矢量投影计算停留时间，如下所示（有效区间 ):
 

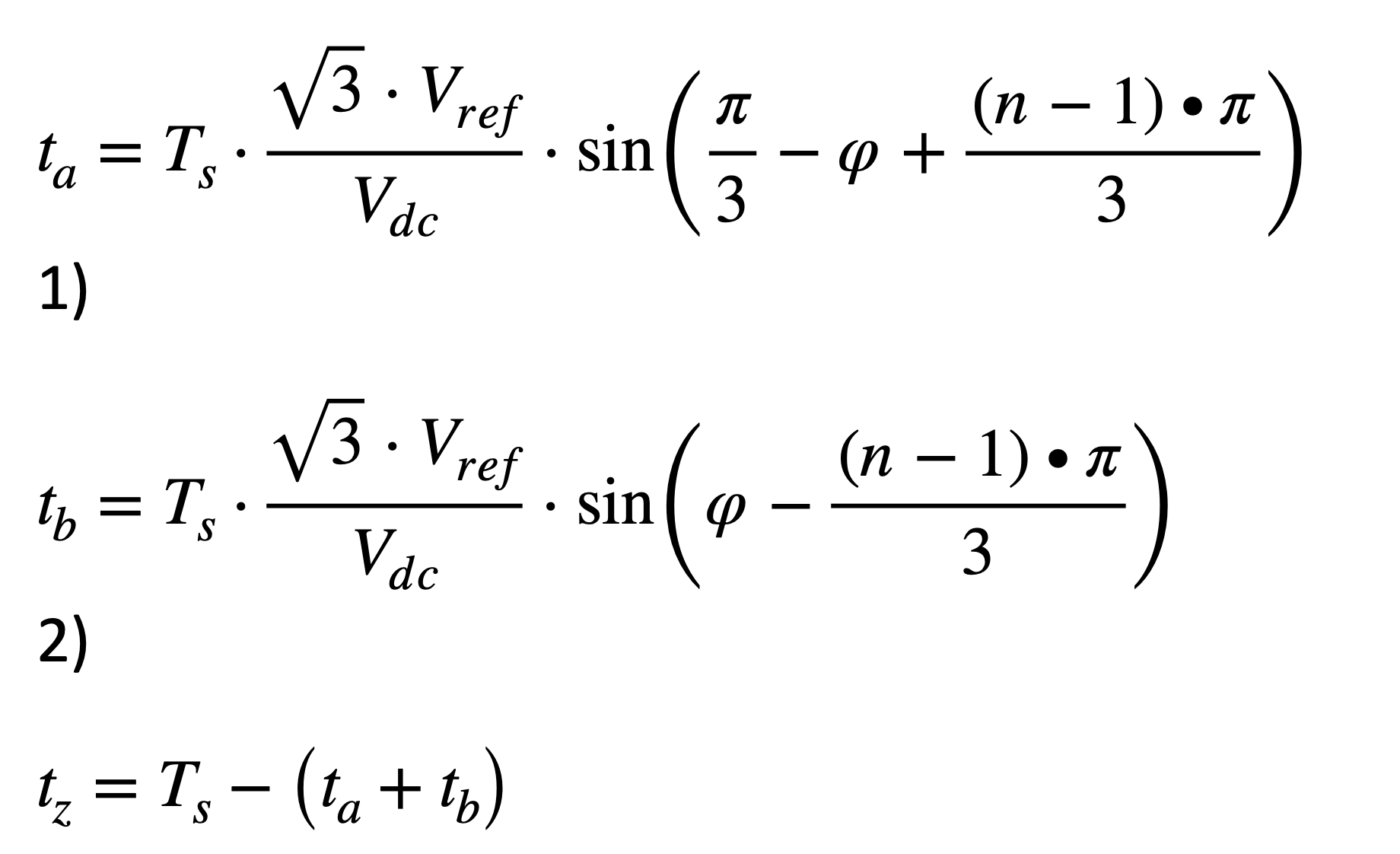
（方程1） （方程2） （方程3）

磁场定向控制（FOC）：

磁场定向控制（FOC）可以理解为电机扭矩的瞬时调节。瞬时扭矩方程是磁链矢量和电机电流矢量的函数。 

该过程基于参照框架理论，支持设计人员将复杂的三相系统分解为与电机同步框架相关的 dq 系统中的等效模型。因此，该算法无需操纵三相量（电流和电压），而是必须控制两个直流项，一个与扭矩（q 轴）相关，另一个与磁通（d 轴）相关。 

图 9 代表系统参照的转换和变化。关于 Clarke 变换、Park 变换和所有数学操作的说明超出了本文档的范围。αβ 轴相互垂直，并固定在同一位置。另一方面，dq 轴以同步速度旋转。电机磁通位置与 d 轴对齐。
 

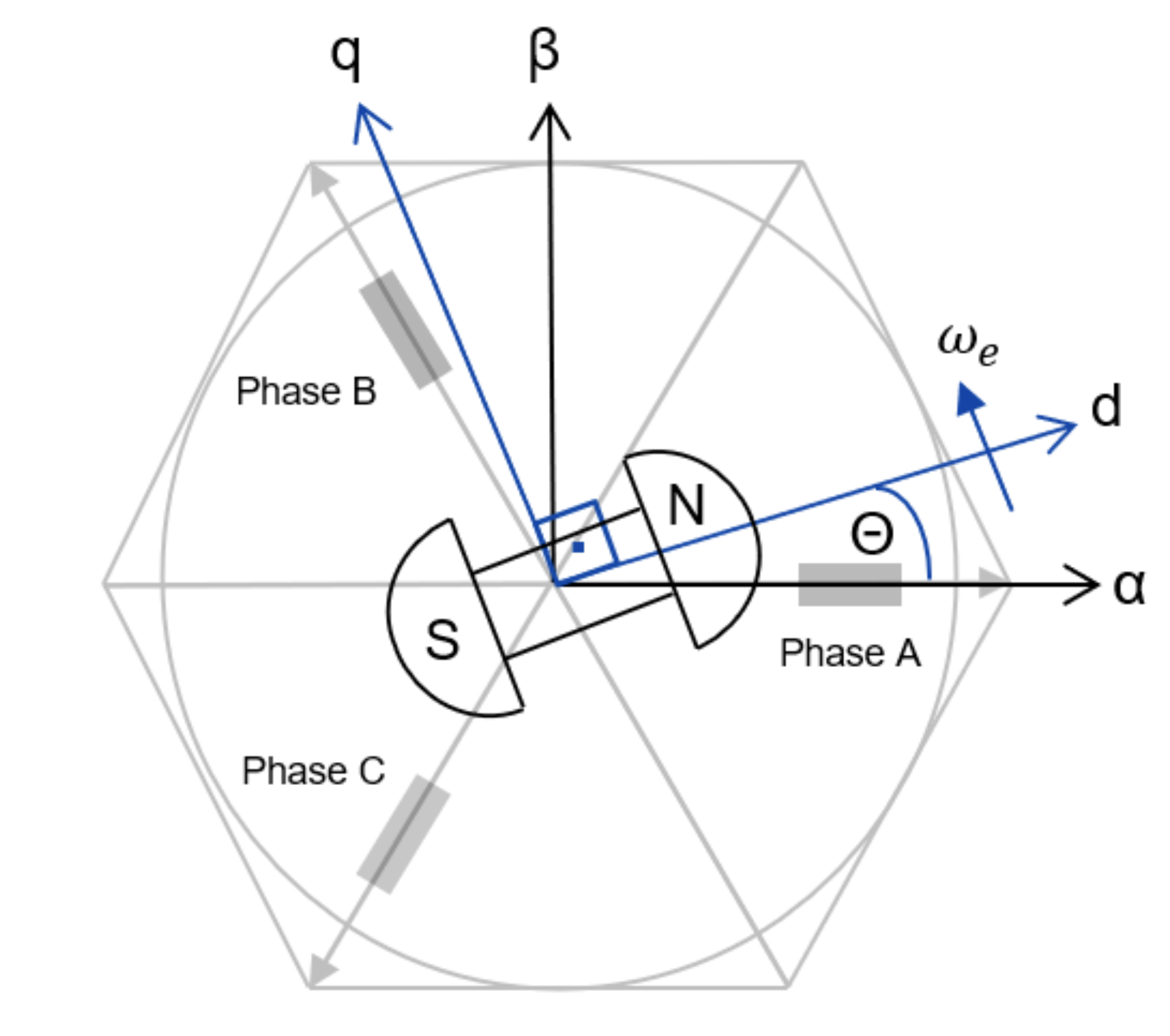
图 9：参照框架理论应用于 BLDC 机器。

图 10-a 描绘了 FOC 速度控制回路（q 轴）的块状图，而图 10-b 则显示了磁通调节器（d 轴）部分。速度控制器的输出被称为 q 轴参照电流，反过来会向内部电流调节器供电，从而生成 q 轴参照电压。因为 q 轴和 d 轴之间的交叉耦合项，在调节器回路中需要将其考虑在内。补偿的方法有很多，可以使用前馈方案来抵消该项，或者使用最快回路是 d 轴调节器的串联调节器设计。 
 

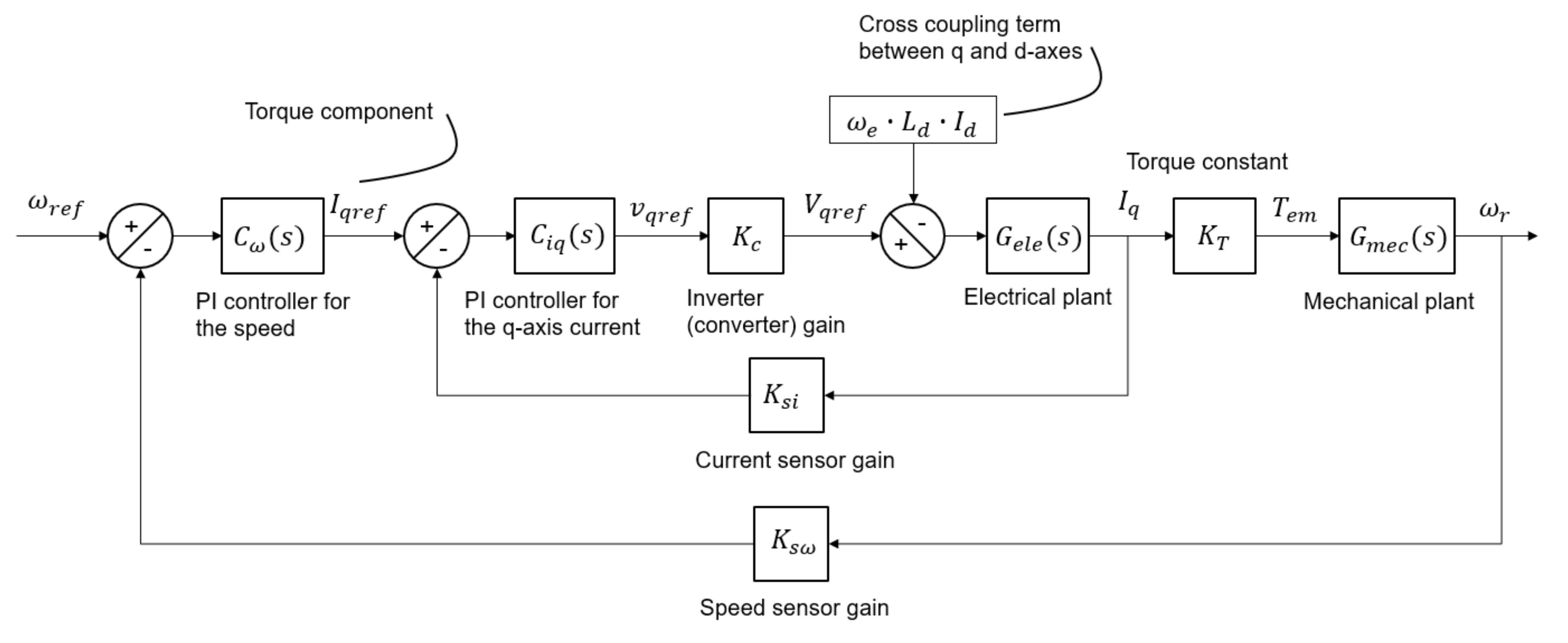
速度和扭矩调节器（q 轴）。

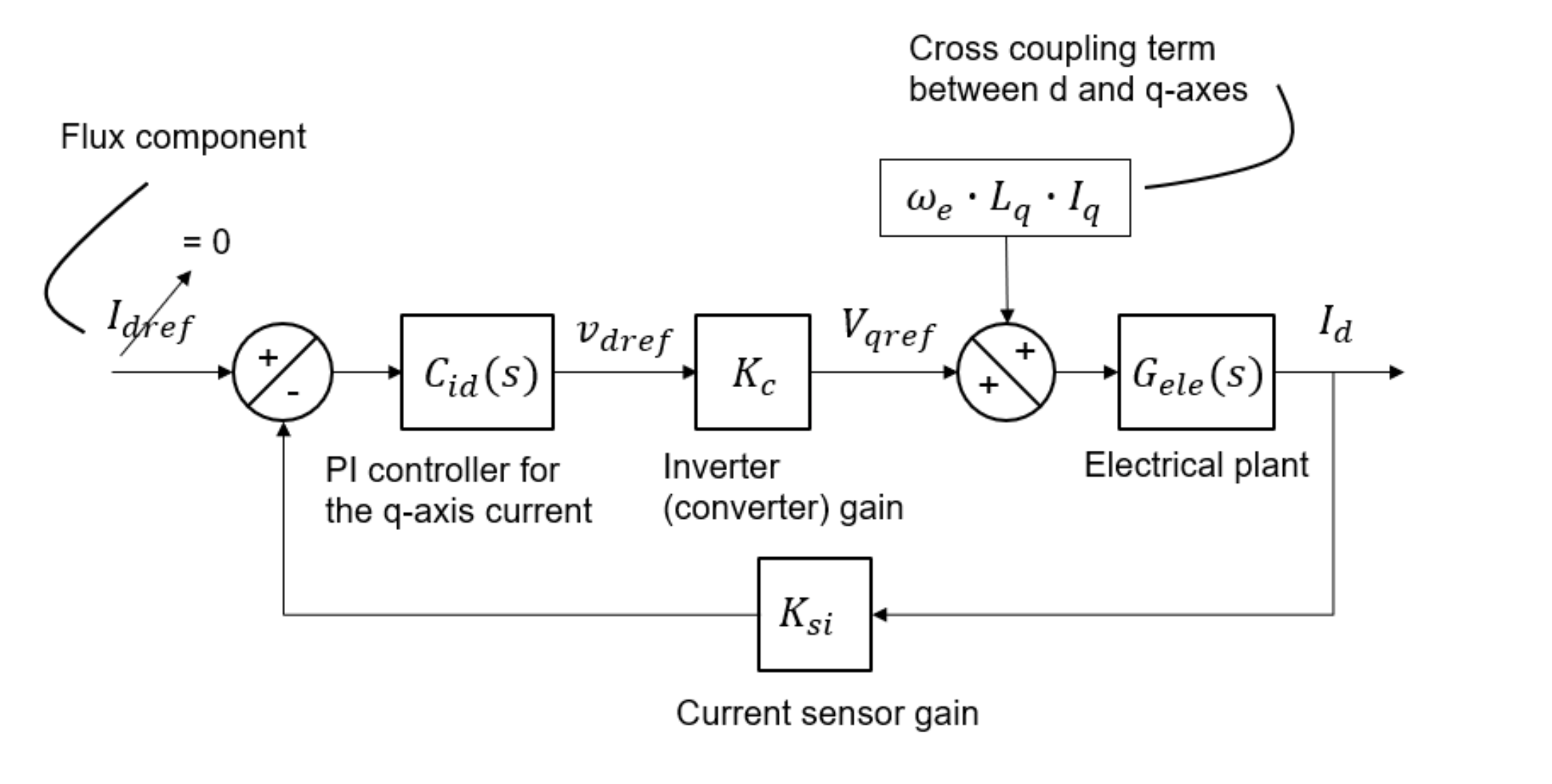
磁通调节器（d 轴）。

图 10：两个轴的 FOC 块状图。

最大每安扭矩（MPTA）和磁场削弱（FW）：

最大每安扭矩（MPTA）是最大限度地减少机器中的铜损的技术，适用于已经制定的 FOC 调节器方案。图 11-a 的相量图演示了这个概念。在这种运行模式下，电机电流矢量和电机磁场保持相互垂直，从而实现扭矩最大化。 
 

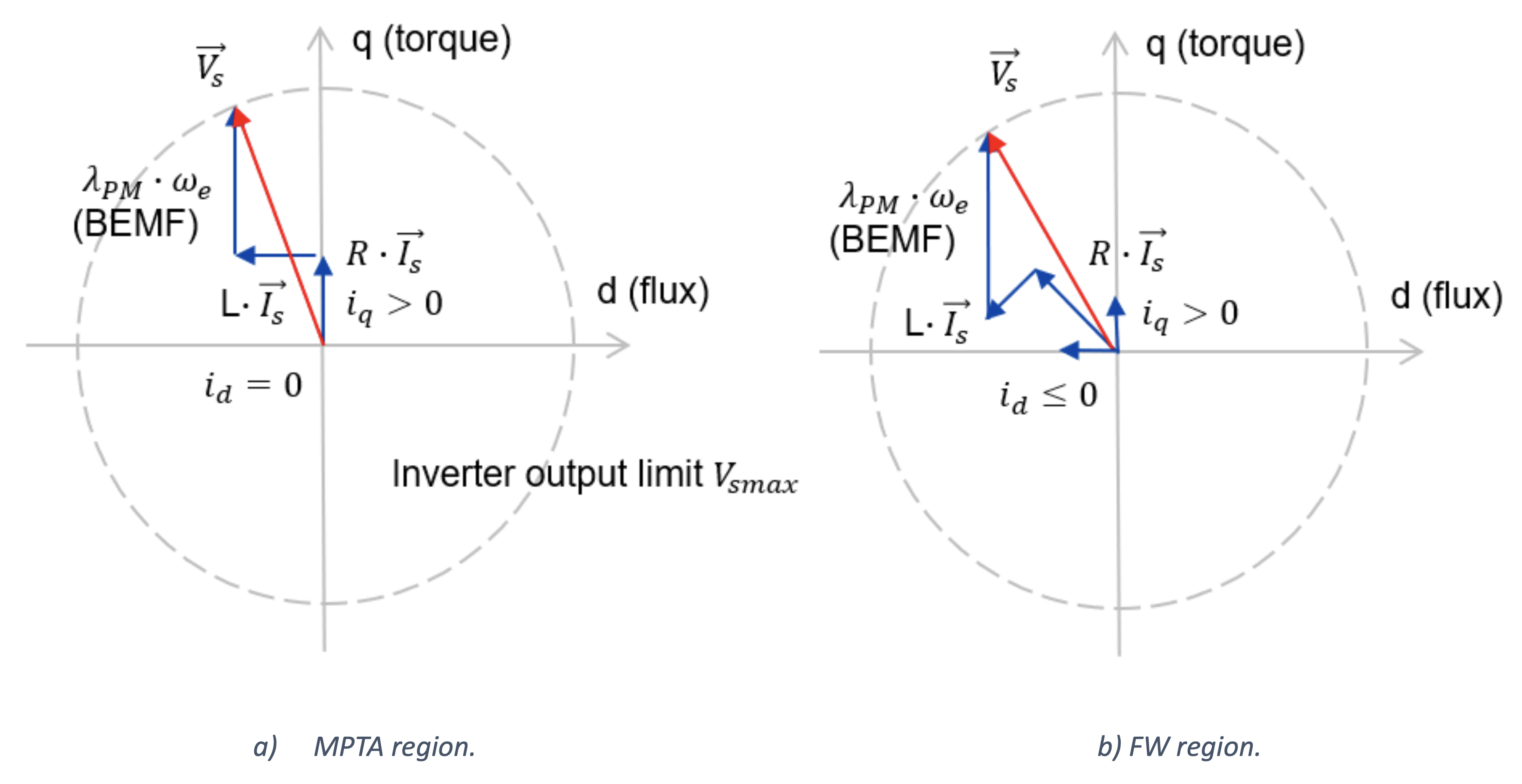
图 11：电机相量图。

尽管最大化扭矩可以确保更高的效率，但存在物理限制，并且如果电机速度超过基本速度，则电机无法在 MPTA 下运行，因为没有足够的直流链路电压来克服电机 BEMF。

这个问题的解决方案可在方程 4 中所示的扭矩方程中找到。d 轴磁链有两个分量，其中一个是因为永磁场。符号惯例是这样的，对于负 I_{d 电流，第二项从 PM 磁通中减去，这对于电机运行而言是正确的，如} I_q ≥ 0 and I_d ≤ 0。

（方程4）

针对确保 MTPA 的算法，将参照 d 轴电流设置为零。原因是它不该抵消 PM 磁通。另一方面，如果机器超过了基本速度，参见图 11-b，则必须为那一对 (I_q , I_d) 选取适当的值，以确保部分隐藏 PM 磁通项，从而克服逆变器限制。这种操作模式称为磁场削弱（FW）。

基本速度的定义使用方程5 表示，其中 V_{s_max} 表示最大逆变器输出电压（取决于调制方案），I_{s_max} 表示最大逆变器电流或名义电机电流（以最小者为准）。

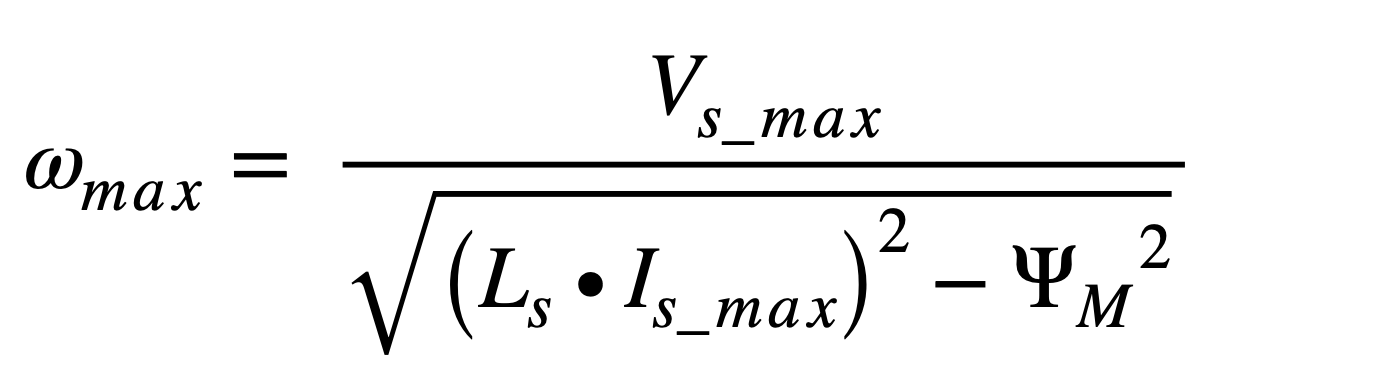
（方程5）

单分流电流测量：

在需要无传感器操作的几十瓦到几千瓦的应用中，单分流器电流测量是一种非常热门的方法。它可以大幅降低材料清单成本。此方法的另一个优点是无需担心 ADC 信号路径（2 相或 3 相电流感测）的匹配，因为所有电流都将使用相同的 ADC 通道进行采样。下一节将说明使用 SVM 测量电流的必要性。 

图 12 展示了具有中心对齐的 PWM 的 SVM 调制示例，用于在 V5“011”到 V4“001”之间的转变。在此分区内，相电流 u 和 v 为负，而 w 为正。只有当相应的 LS 开关打开时，每个逆变器桥臂才会携带电流，即用于 PWM 周期（1-D）的补偿。因此，三个单独的逆变器桥臂电流的总和等于单分流信号。当然，如果应用“000”或“111”空矢量，则没有信号。
 

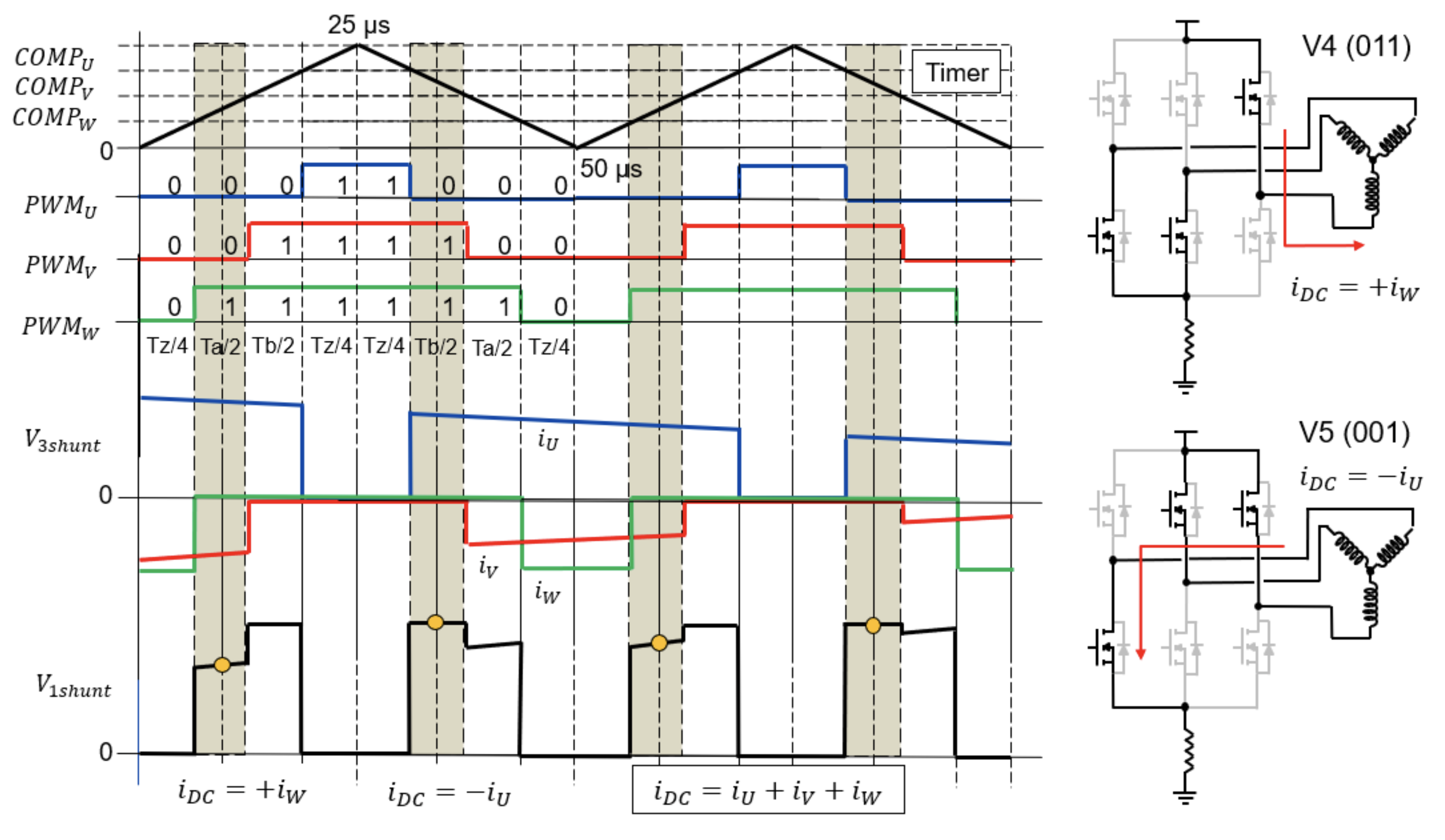
图 12：具有中心对齐和单分流电流信号的 PWM 的 SVM 调制，表示分区 5 至 0。

位置观测器：

随着应用功能的提升，其性能要求也随之提高。因此，使用普通的六步调制很难满足标准。相反，设计人员必须选择支持 SVM 调制。此外，由于成本限制，这些应用通常需要无感操作。但是，由于在 SVM 方法中没有悬空相位，因此不再可能进行直接 BEMF 传感来确定确切的 ZC 瞬间。 

从这个角度来看，文献（以及业内）中出现了许多转子位置估计器算法，以支持机器在使用 SVM 调制的同时进行无感操作。为了执行此类算法，软件需要了解动态的电机电压和电流以及其他电气量。因此，上一节关于分流电流检测的内容至关重要。

在文献提供的各种估计方法中，电压模型是最著名的一种（部分作者称之为磁通估计器）。它以电机电压方程为基础。通过电机电压方程可以获得电机磁链，从而确定转子角位置。尽管很简单，如果电机参数众所周知，并且机器电流和电压测量值误差很小，则该算法可以提供良好的结果。

在低速启动的状态下，传统的无感方案往往会受到影响。由于方程取决于磁通，并且此时的 BEMF 太小，因此测量误差会导致信噪比（SNR）降低。为了应对这种无能为力，许多修正或增强方案得以提出，以创建混合估计器，一个适合低速，另一个适合高速，甚至不同类型的估计器。 

步进电机属于 BLDC 电机，将完整旋转划分为增量步骤。由连接到 H 桥的线圈组成的双相步进电机可提供准确的定位。步进电机可提供步进模式，包括全步进、半步进、调整半步进和微步进，每种模式都会影响扭矩、准确性和运动。
 

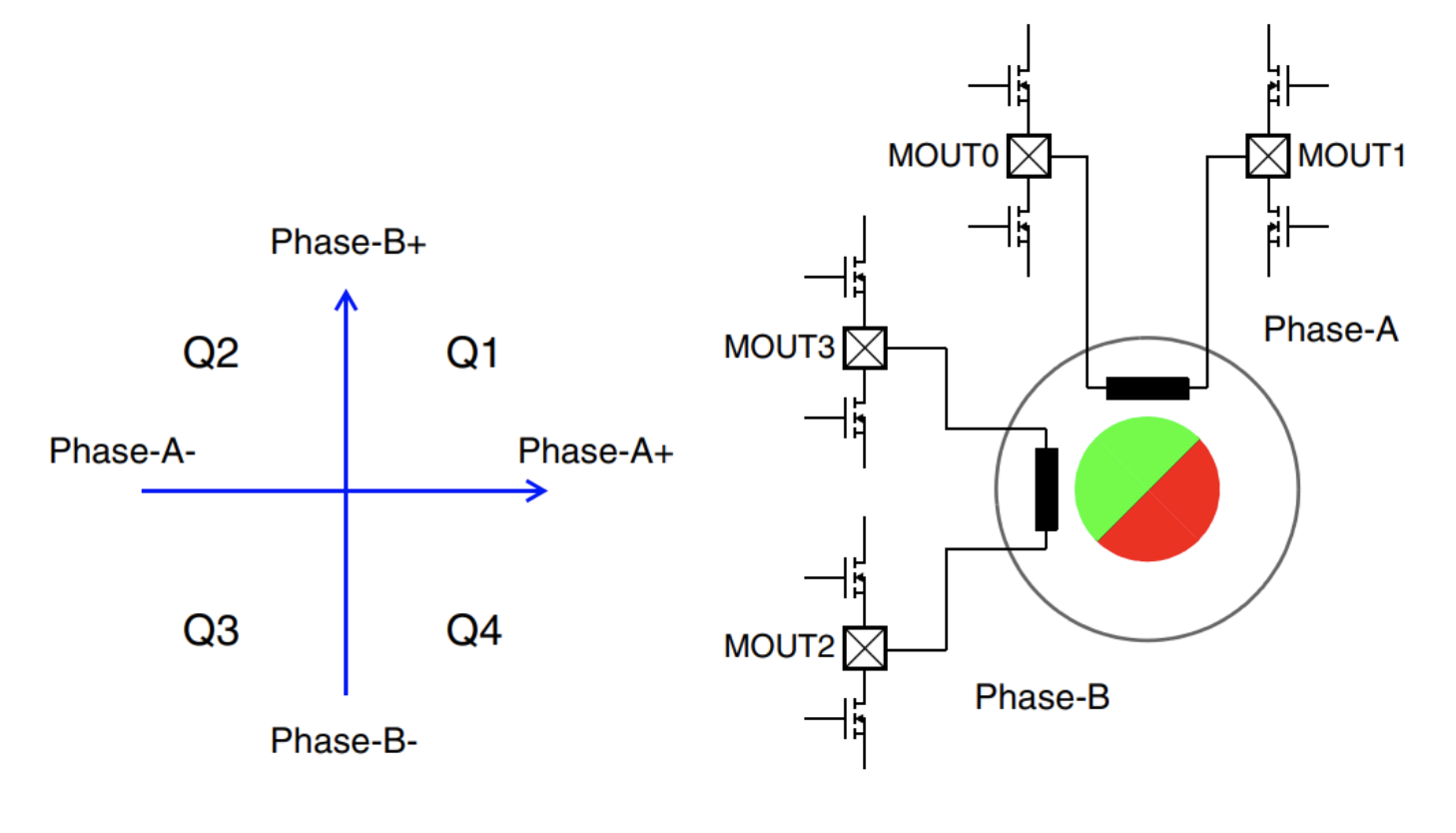
图 6：双极步进电机电路

步进模式：探索全步进、半步进、调整半步进和微步进模式

步进电机通过不同的步进模式运行，具体取决于来自控制器的脉冲命令数量。 

在全步进模式下，电机的两个相位均通电，每一次电旋转支持四个步距。
 

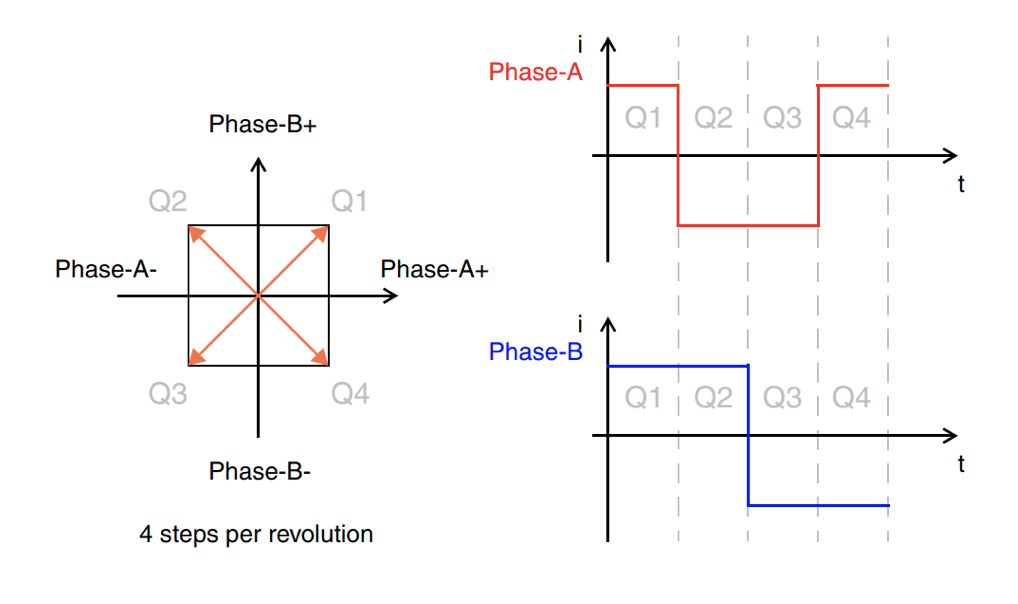
图 7：全步进模式

半步进模式在全步进模式之间插入中间步进，每次旋转提供八个步距。 
 

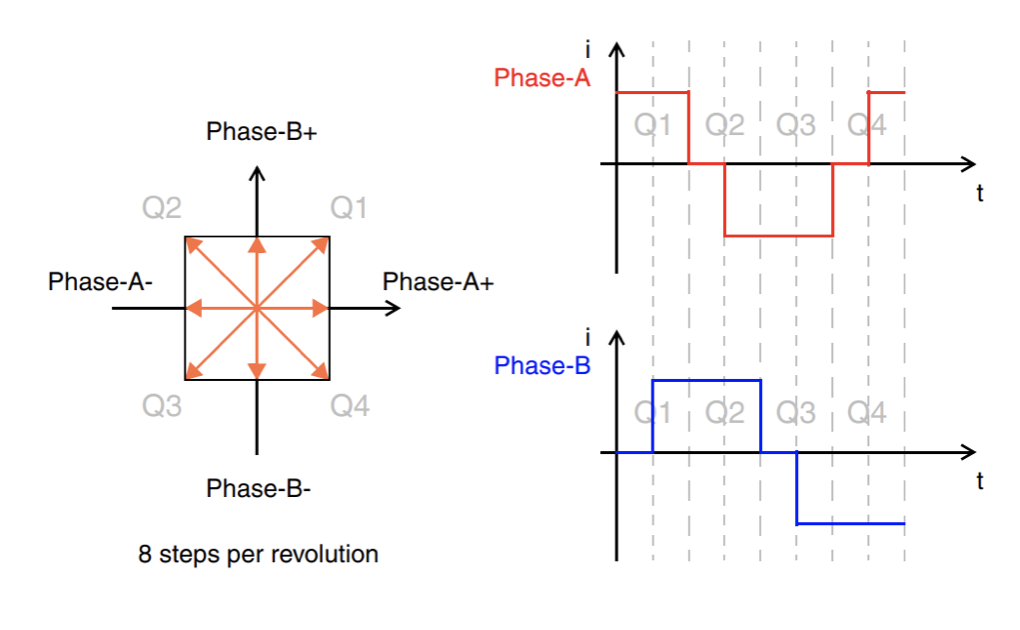
图 8：半步模式

调整半步进模式在中间步进期间调整电流矢量，以最大限度地减少扭矩波动。 

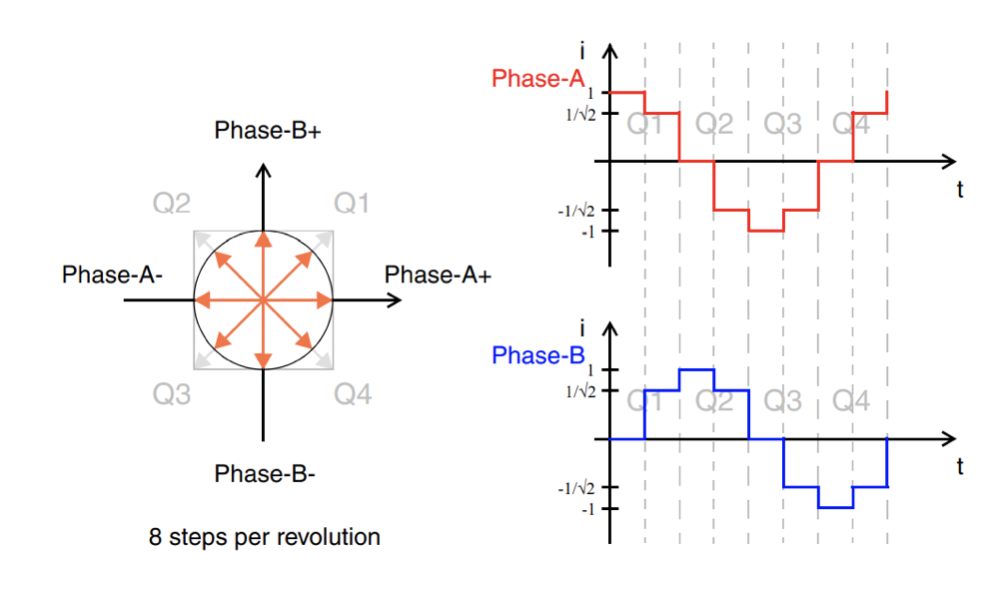
图 9：调整半步进模式

微步进模式采用正弦/余弦形电流，支持多功能矢量形成，分辨率由每个全步进或象限定义，通常每个象限最多 32 微步距。微步进分辨率由应用软件中的正弦表确定，可实现各种步宽的精确控制。

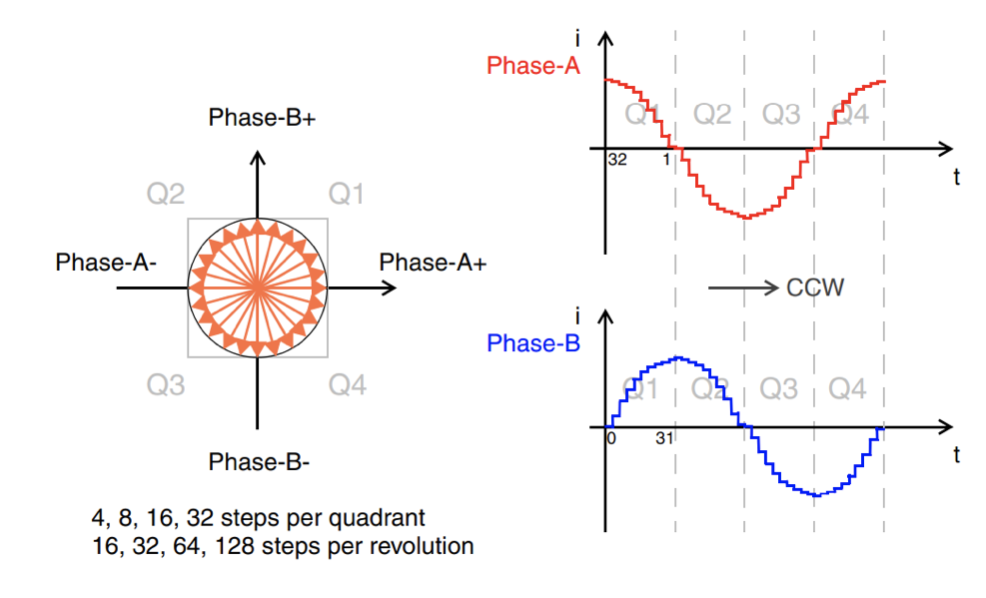
图 10：微步进模式

电流衰减：管理电流衰减以实现微步进的最佳性能

为了在电机的整个速度范围内实现用于微步进的正弦电流波形，有效的电流衰减控制至关重要。目标是最大限度地减少电流波纹，以减少排放并降低声学噪音。该方法涉及根据电机速度和电流水平调整电流衰减策略。

在低速和低电流场景中，异步缓慢衰减是首选模式。当 H 桥中的开关关闭时，空转电流会流经相同桥臂中对向开关的本征二极管。这种衰减模式对于低速和低电流水平下的上升或下降电流特别有效。

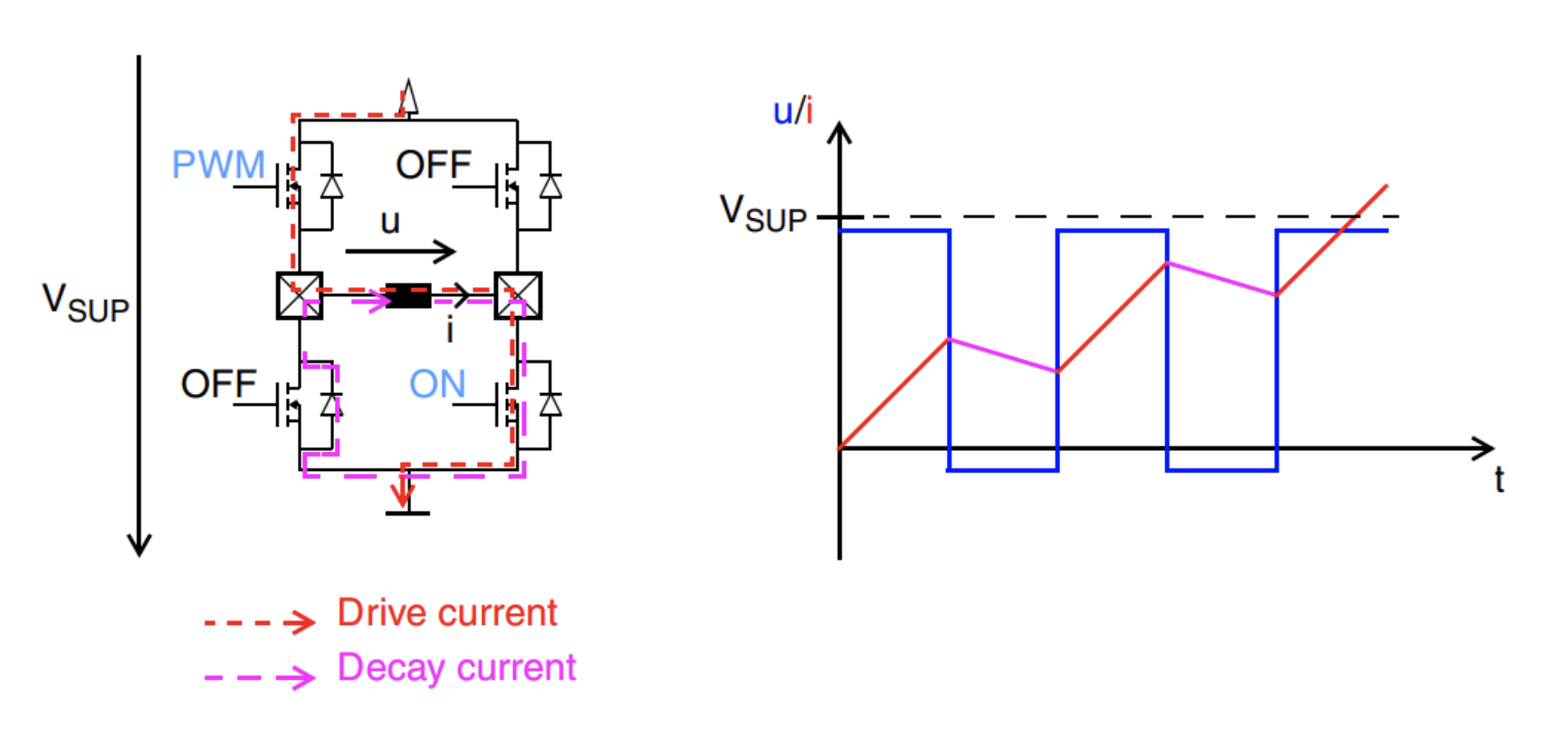
图 12：异步缓慢衰减

对于高速和高电流情况，同步快速衰减是最佳模式。在此模式下，H 桥中的两个导电开关同时关闭，而相应桥臂中的对向开关则会打开。空转电流通过激活的开关流回电源。这种衰减模式非常适合涉及高速和高电流水平的下降电流的场景。
 

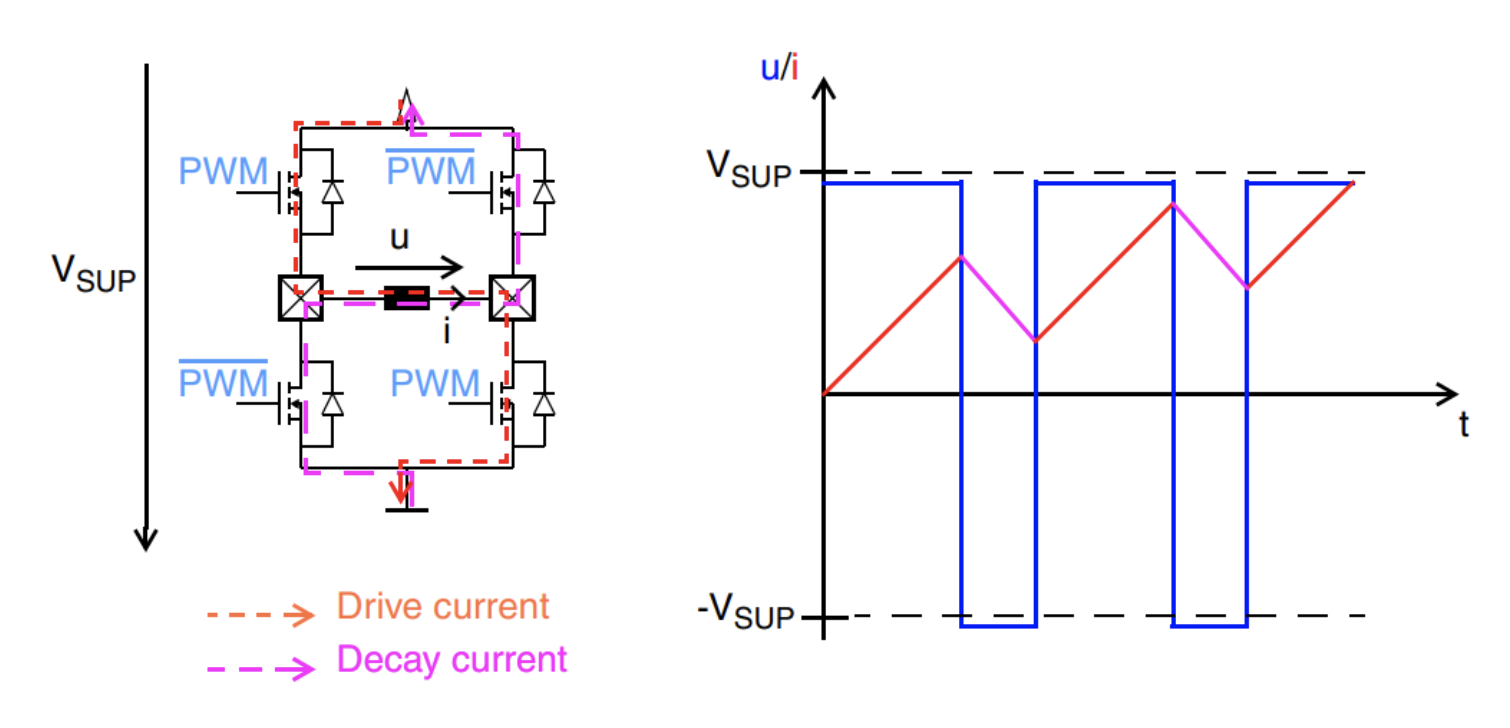
图 13：同步快速衰减

在电机速度和电流水平不同的情况下，混合衰减（快速和缓慢衰减的组合）已得到有效性证实。这种方法涉及首先应用快速同步衰减，然后在一个 PWM 周期内应用同步缓慢衰减。混合衰减的比率可以适应电流水平和电机速度。混合衰减是在中高速和高到低电流水平下减少电流的首选模式。
 

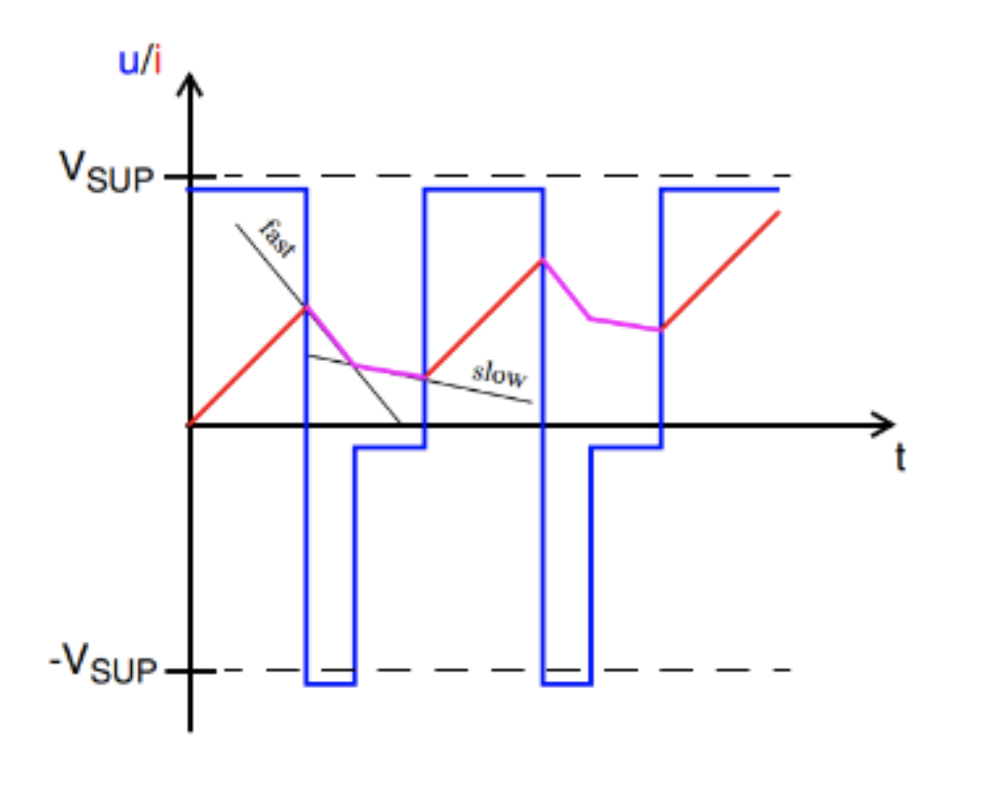
图 14：混合衰减
 

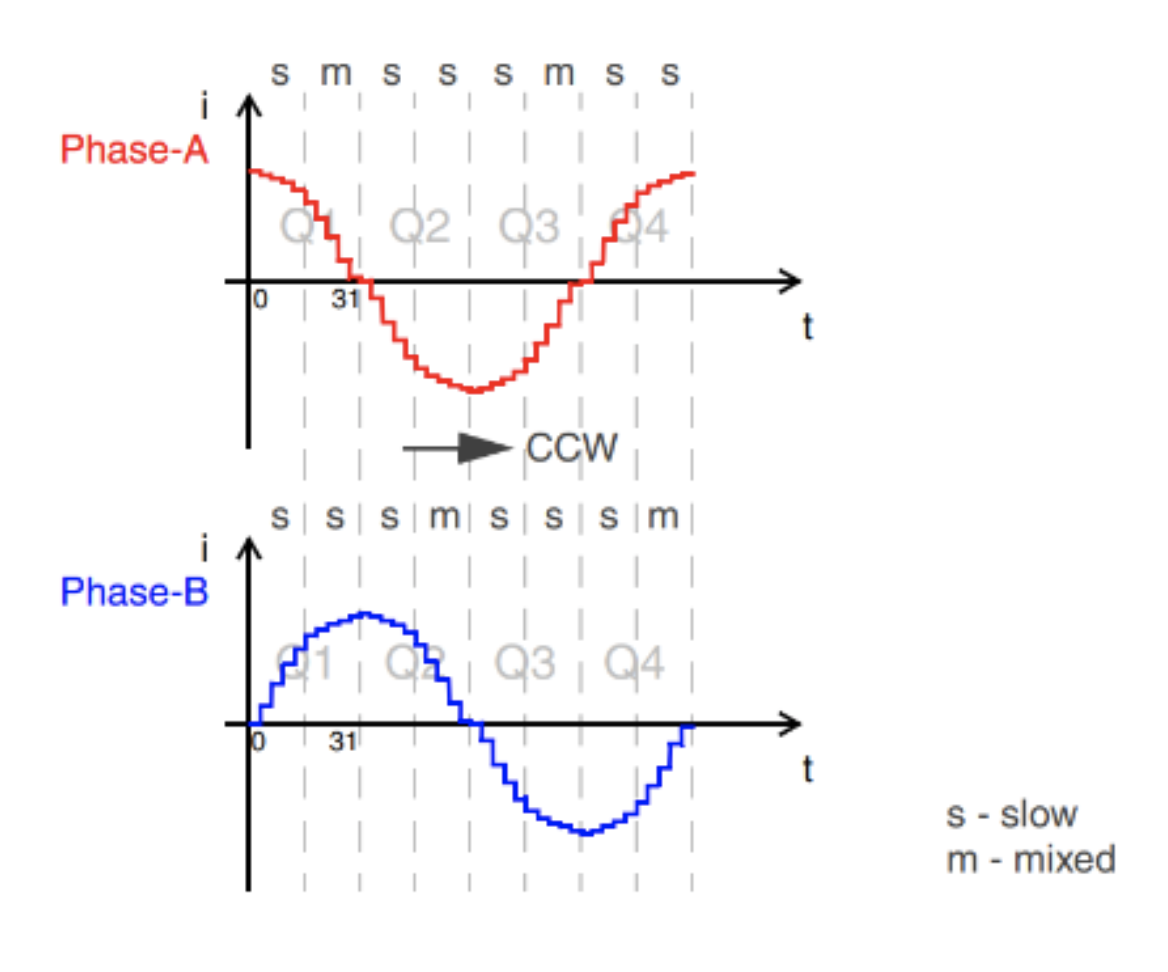
图 15：微步进模式下缓慢和混合衰减应用的示例

通过在应用软件中实现快速衰减和缓慢衰减之间的固定比率，可以确保最佳性能。此外，谨慎定义的电流阈值可以防止电机在低电流水平期间逆转，当设置的电流水平低于该阈值时，会应用缓慢衰减。

失速检测：监控 BEMF 电压以检测失速并防止步损

失速检测通过 BEMF 电压测量来实现，尤其是在微步进模式下。在此模式下，BEMF 电压与电机速度成正比，从而可以直接识别电机是否处于运动状态。不过，由于测量仅在一相未通电时进行，BEMF 电压的视图会受到限制。在没有负载和损耗的理想情况下，BEMF 电压峰值与零相电流点一致。在施加负载的现实条件下，电机滞后于电机场，从而产生了与负载相关的相差。这种滞后导致 BEMF 电压从峰值（指示零扭矩）到过零点（指示失速扭矩）的移动。这种转变意味着失速和步损。
 

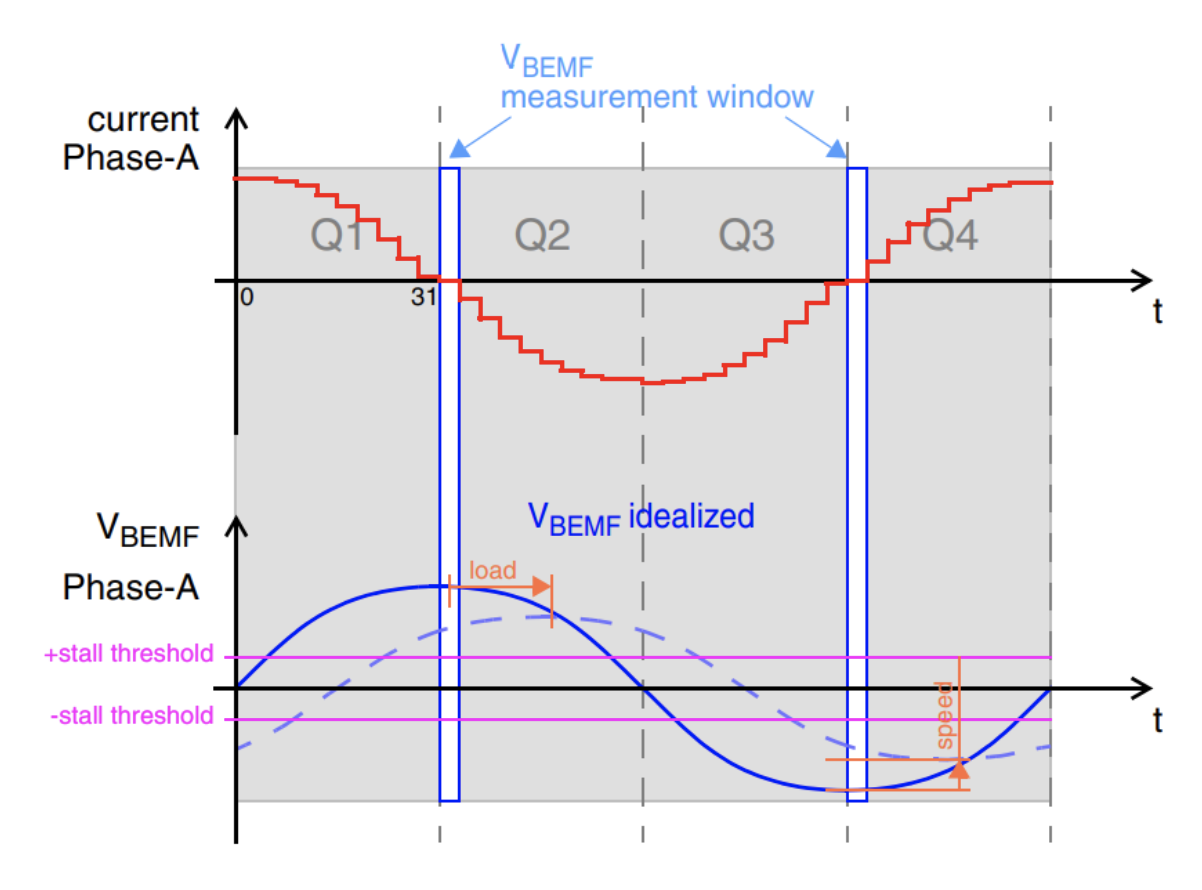
图 17：用于失速检测的 V_BEMF 测量